在企业中平行的组织间有各种维度的指标考核,这些指标权重不同,单位不同,评优趋势也不同,比如制造业中,集团下属的多个工厂都有人效类,成本类,质量类,安全类等多个指标,这些指标单位都各不相同,有的指标数值成千上万,有的是小于1的百分比,还有的是个位数的发生次数,指标之间的对标存在困难,而且一些指标是越大越好,比如人员效率、设备效率、产品合格率等;一些指标则是越小越好,比如客户投诉件数、安全事故件数、关键岗位的人员流失率等;更有的指标是需要维持在某个水平,比如质量成本、、直接产出人数与管理人数比等。同时各个工厂的指标表现各有优劣,比如有的工厂产量高但安全事故偏多,制造成本表现不凡但员工流失率较高等,横向对比起来会让管理者绞尽脑汁的制定各种排序规则,其最终目的都是将各种指标调整到同一个“频道”上来,便于累计求出总成绩,进而排序评价。类似这种评价烦恼同样存在于经济类、社会等模糊性系统的排序与评价。
1982年我国学者邓聚龙教授根据控制论中信息明晰程度的黑白灰系统表达方式,提出了灰色系统理论,即一种信息不明确的系统,未知信息的确定依靠的是已知信息。灰色系统理论的优点在于不需要大量完整的信息便可以处理多因素、非线性的问题,灰色关联分析法是其实现功能的主要方法。灰色关联分析指的是利用灰色关联度来分析确定各个因素间的影响程度,或者是测量各因素对系统主体贡献度的一种方法,它的原理是依据序列曲线的几何形状相似度来描述因素间、因素与主体间的紧密性。简单来说,文章开头描述的那些模糊的评价麻烦,可以在灰色关联评价法中轻松避免,无需繁琐的换算规则,无需大量的完整信息,无惧维度众多的评价指标。
下文将概述灰色关联评价模型的运算步骤,并结合一个制造型企业各车间年终评比的小案例,来介绍应用MCE决策软件中的灰色关联评价模块一键生成排序结果。
评价排序决策过程分为构建模型和计算两个部分,其中模型构建分为两个步骤:
1. 构建评价指标矩阵
2. 选定最优指标集(也可称为最优序列和参考序列)
模型构建完成后的计算分为五个步骤:
1. 构造初始矩阵
2. 数据进行无量纲化处理
3. 确定评价矩阵
4. 确定各指标的权重矩阵
5. 计算评价结果
由于模型的构建和计算需要更大的篇幅和感官上复杂的矩阵展示,在本文中就不做详细讲解了,感兴趣的读者只要搜索资料,仔细的结合教材案例按步骤进行矩阵运算便可理解,更何况在现实的决策情境中,指标项目和评价对象的数量都很多,构建庞大的矩阵并按步骤进行运算,不仅需要一定的时间和数学基础,而且在过程中也容易发生数据错误,这就违背了使用这套简便方法进行评价、排序、决策的初衷。当今时代,好的方法一定不会被繁琐的计算而湮没,现代综合评价方法MCE软件便解决了运算的问题,该软件大小不到6兆,价格合理,其中包含AHP、FUZZY、GARY三个模块,灰色关联评价模型就是其中的GARY模块。下文将以某工厂2021年四个生产车间的管理水平评价为例,展示下灰色关联评价方法的操作过程:
1. 基础数据
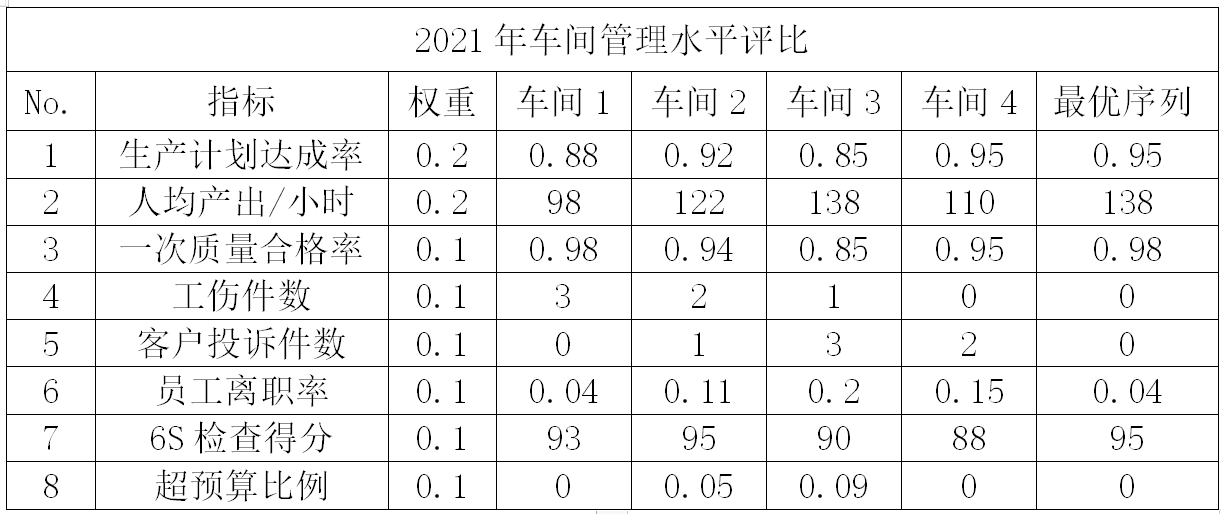
2.打开软件,构建评价对象与指标模型
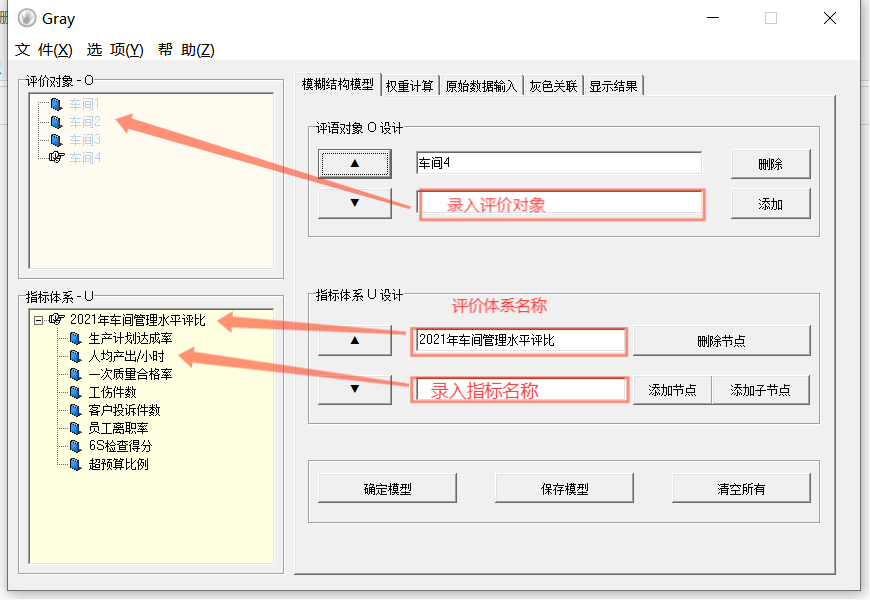
3. 手动输入指标权重
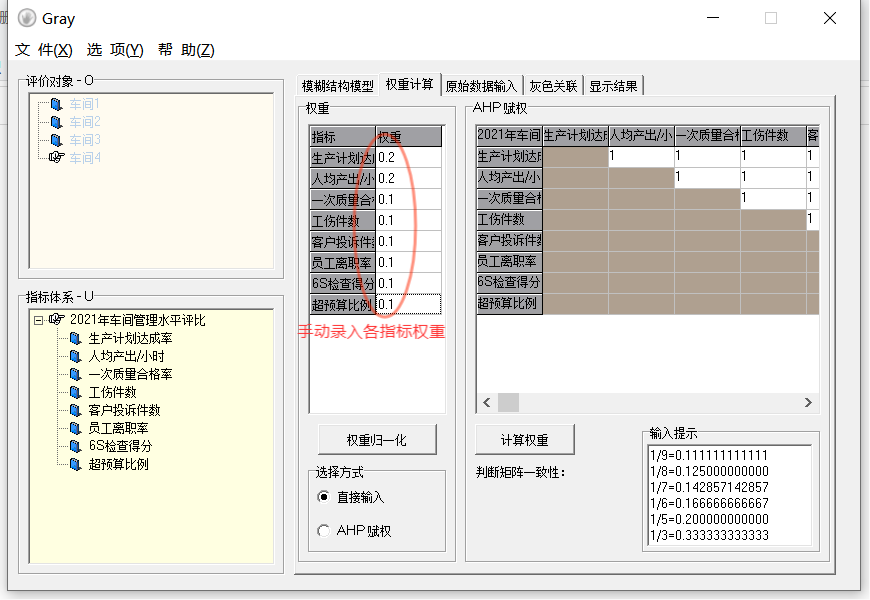
4. 录入指标数据和参考序列(最优序列),查看数据图例
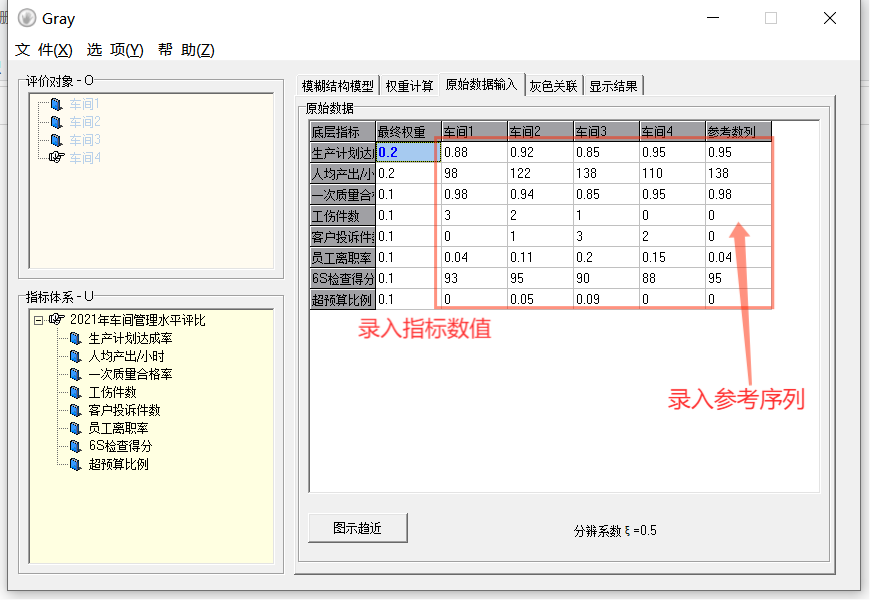
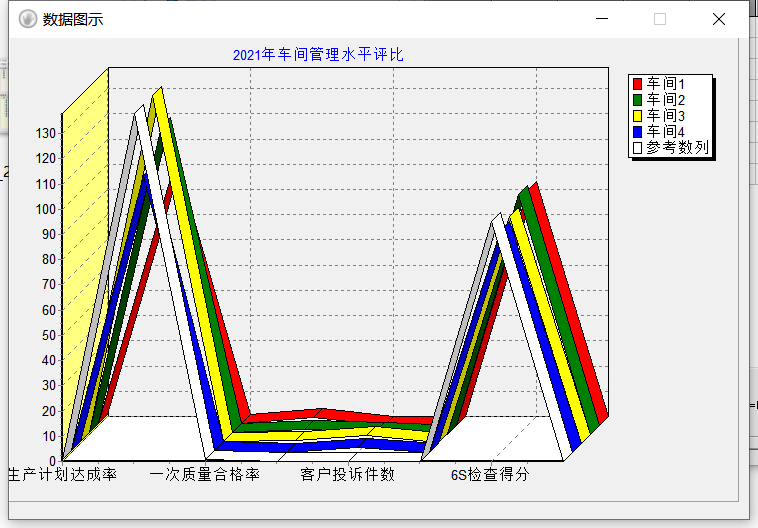
5. 点击计算关联系数
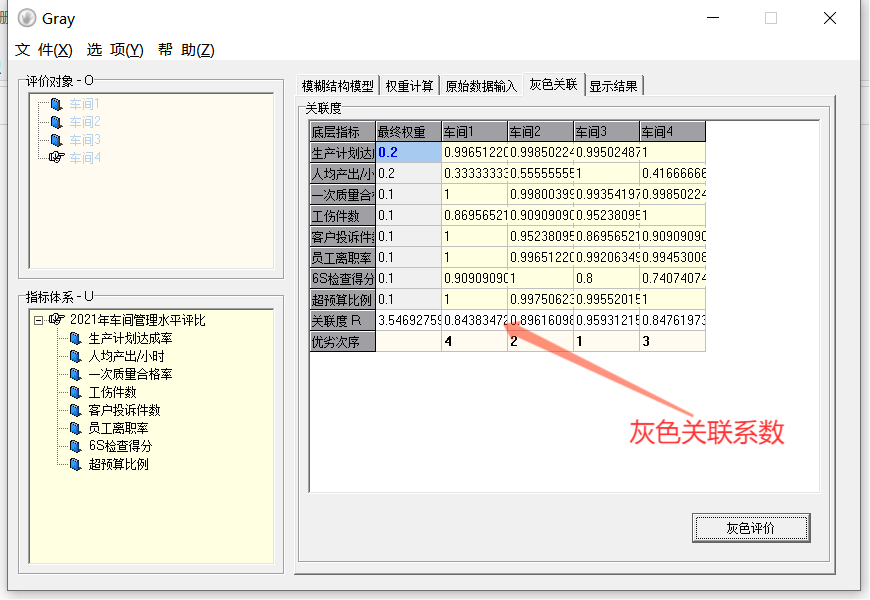
6. 输出评价排序结果
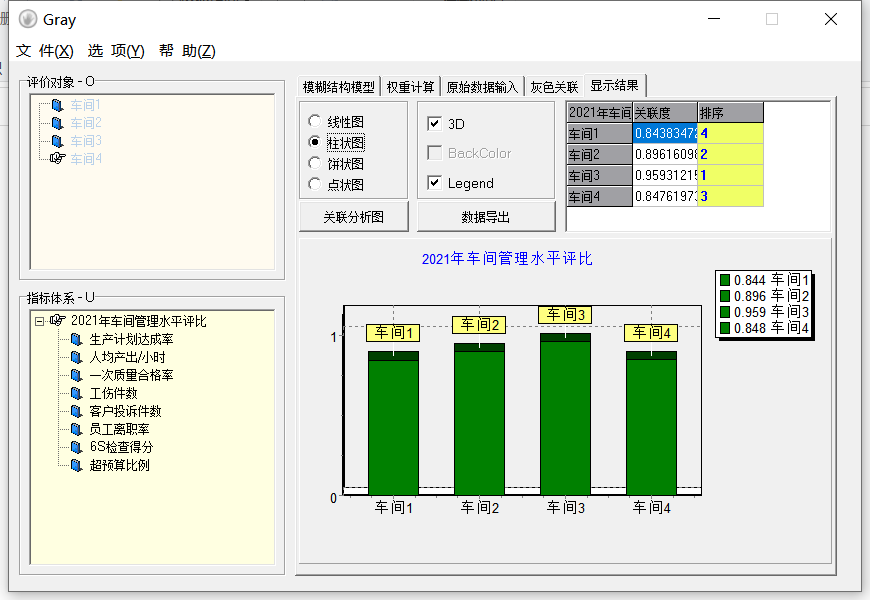
从图中可以直观看到评价排序为:车间3、车间2、车间1、车间4。
软件还支持AHP层次分析法确定权重功能、排序多种目视化图表展示和数据导出,希望本文可以为读者提供评价方法思路上的启发,详细的灰色关联评价模型与方法的原理和计算过程可以从网上搜索学习。
本文为冠卓咨询原创文字作品,任何人或组织不得对本文进行篡改,转载或以盈利为目的行为,一经发现,将负法律责任。