利特尔法则由麻省理工大学斯隆商学院的教授John Little﹐于1961年所提出与证明。法则的内容是:产品的生产周期(Total Product Cycle Time- TP/ct)=存货数量×生产节拍。TP/ct是指从接收原材料到产品发运所花费的最长路径时间;存货数量是指原材料、在制品和成品的数量;生产节拍是指每生产一个产品所要的时间,流水线上一般等于瓶颈时间。
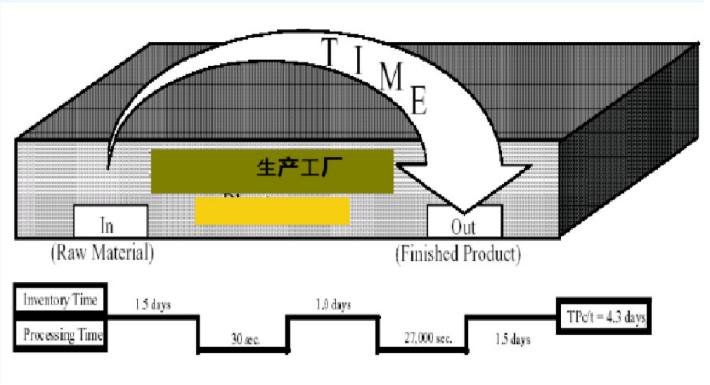
这个公式简单的阐述了TP/ct与存货的关系,也为制造系统缩短TP/ct指明了方向。一个方向是提高产能,从而降低生产节拍。另一个方向就是压缩在存货数量。所以在制造现场,我们要重点关注三库一制程,原材料库、半成品库、成品和瓶颈制程。该法则可以在整个系统中使用,也可以在子系统中使用,如生产交货期=在制品数量×生产节拍。
接下来我们看下利特尔法则在生产中实际应用案例:
案例1:利特尔法则使用
如果客户甲需要100个A产品,而此时产线正在生产A产品,瓶颈时间是10分钟,那么50个A产品的生产周期就是50x10=500分钟。如果此时恰好客户乙需要100个B产品,也是使用这条产线进行生产,瓶颈时间是10分钟那么就需要将客户甲的生产完再生产乙的产品,交货期就是(50+100)x10=1500分钟。
案例2:应用利特尔法则确定极限在制品
库存是一种负债,是成本的消耗,所以库存应该越小越好,但是库存可以应对波动,以防止波动影响系统的稳定运行,所以需要有适量的库存。利特尔法则可以给出库存的最小值,小于这个值,系统便不能稳定输出。
根据利特尔法则,在制品数量=交货期÷生产节拍,如果一条生产线有4道工序,每道工序所需时间分别是7分钟,8分钟,10分钟和8分钟,那么这条产线的时间长度是33分钟,瓶颈时间是10分钟。在制品的极小值是33/10=3.3个,也就是4个在制品。如果在制品的数量小于4个,那么系统不可能以10分钟每个的稳定速度输出。因为如果是3个在制品,就不可能以10分钟每个的速度产出了。在精益生产中,流水线生产和TOC制约理论都是先给定一个缓冲值,然后不断减少这个缓冲来寻找限制流动的因素,消除流动因素后,继续缩减缓冲,寻找下一个限制因素。
本文为冠卓咨询原创文字作品,任何人或组织不得对本文进行篡改,转载或以盈利为目的行为,一经发现,将负法律责任。