多变异分析:车床与工人到底该改善谁?
实施六西格玛管理的一个重要目标就是要减少生产过程中产品关键质量特性的变异,即生产出的产品特性指标的标准差尽可能小。当然,减小标准差可不是件容易的事,生产中产生变异的原因可能很多,一般的做法是:通过事先安排好的计划,有规律地去收集生产过程中的有关数据,通过分析,定量地给出每部分变异在总变异中的比例,作为选择改进措施时的依据,这就是多变异分析。
下面我们通过两个例子来说明:
例1:
生产车床关键部件之一的丝杠时,最重要的指标是直径。为了研究变异产生的原因,选了3名工人(他们各自拥有自己固定的车床),让他们在自己的车床上连续生产出5根丝杠,测量丝杠两端及中部的直径(单位:mm)得到测量结果。试分析变异产生的原因及大小。
多变异分析把变异分为三类:
(1)产品内变异:产品的质量特性在不同位置的变异。上例中同一根丝杠在不同位置测量直径的差异称为产品内变异,一般当做随机误差处理。
(2)产品间变异:不同丝杠直径平均值之间的差异称为产品间差异或组间差异。部件之间、人员之间、原料批次之间、供应商之间、设备之间、方法之间、环境之间的差异都可归于产品间差异。
(3)时间变异:不同时间抽样样本之间的差异。本例中没有考虑不同时间的变异。
多变异分析一般要先画因子图,确定因子之间的关系。根据我们的问题,可以画出以下因子图:
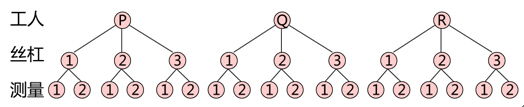
从图中可以看出,导致变异的原因包括工人、丝杠和测量位置。一般说来,在多变异分析中,最底层的重复一定当做随机误差处理。在这个例子中,什么原因会导致同一根丝杠不同位置直径的波动我们不去追究,作为随机误差处理。导致变异的因子有两个:工人和丝杠,并且每名工人都有自己的5根丝杠(在因子图中只画出了3根,但不影响对问题的分析),这种因子关系叫做嵌套关系,且丝杠被工人所嵌套。嵌套关系中的因子有上下级关系,类似于族谱中的父子关系。
多变异分析一般先画多变异图,从图形上看一下不同原因导致的波动大小。嵌套关系在填写因子时,一定要从底层的因子开始填,也就是要先填丝杠,再填工人,界面如下:

得到以下多变异图:
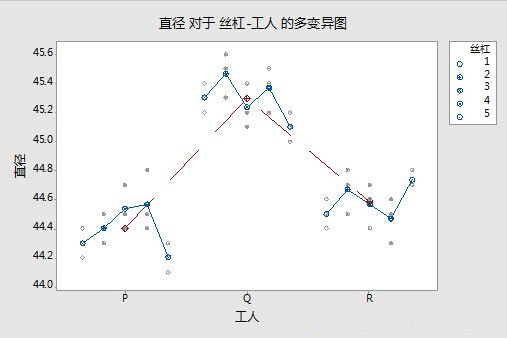
从图中可以看出,不同工人加工丝杠的波动看起来更大。真的是这样吗?我们要进行方差分析,计算方差分量,然后画Pareto图:
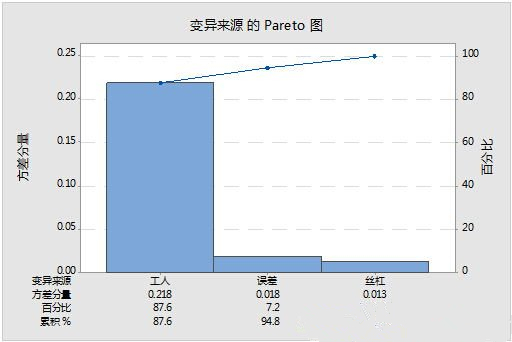
从图中可以看出,工人的方差分量占87.6%,说明工人之间的波动占比最大。如何改善?有人自然会说,要对工人进行培训。真的是这样吗?且慢,这个例子中,我们让每名工人都用自己的车床,数据分析显示工人之间的波动大,完全有可能是车床之间波动大,我们这种抽样方案是无法区分的。所以,为了分清到底是工人还是车床之间的波动大,我们要采用下面的抽样方案(例2)。
例2:
考虑精密车工车间生产微型轴杆长度波动过大问题。从十几位工人中随机选取3名工人,让他们使用同一根钢条作原料,大家都使用固定的已编好号的4台车床,按随机顺序各自分别加工出3根轴杆,然后分别测量其长度,共得到36个数据。我们要分析轴杆长度间产生变异的原因,究竟是车床间的变异为主?还是工人间的变异为主?还是同一工人同一车床生产的不同轴杆间的变异为主?
在这个例子中,工人之间加工的微型轴杆长度有波动,车床之间也有波动,且每名工人都要使用四台车床,所以工人与车床之间是交叉的关系。交叉关系中的两个因子是平级的,没有上下级的关系,所以在画多变异图时,先放哪个因子没有关系。多变异图如下:
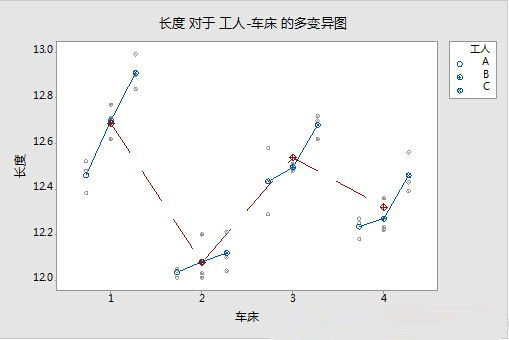
从图中可以看出,车床之间的波动更大。方差分析后得到方差分量,画Pareto图:
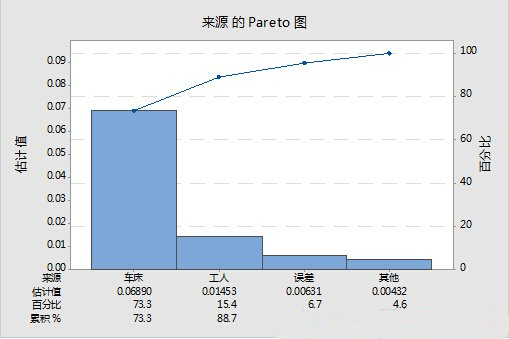
从图中可以看出,车床导致的波动占总波动的比例达到了73.3%,改善的重点应该是车床。
分享:冠卓咨询
说明:转载请注明“精益”